ひとつの球体から次々に生まれた同じ大きさの球体を、ある約束事に従って配置し、それを二次元的に描くとこのような形になります。
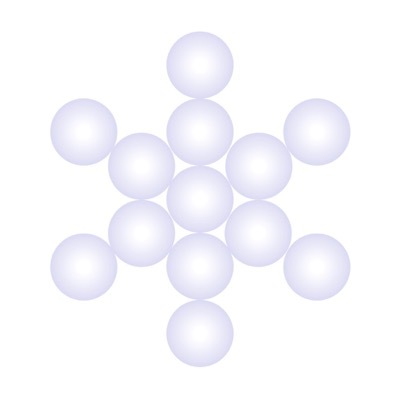
あくまでも二次元に落としただけなので、実際にはここに見えている以上のものが存在するはずなのですが・・・
ここに見えている13の球体の中心を直線で繋ぐと、このような図形があらわれます。
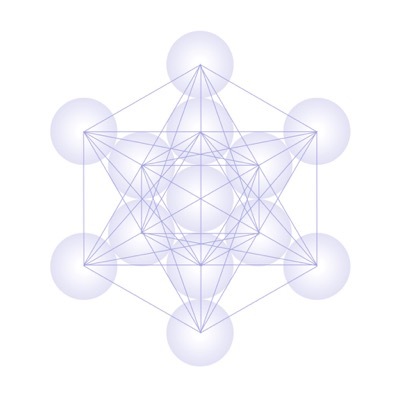
この美しい図形(「メタトロン立方体」とか「メタトロンキューブ」という名称で知られています)の中にはいくつかの立体が隠れています。
そのうちの3つを以下にご紹介しますね。
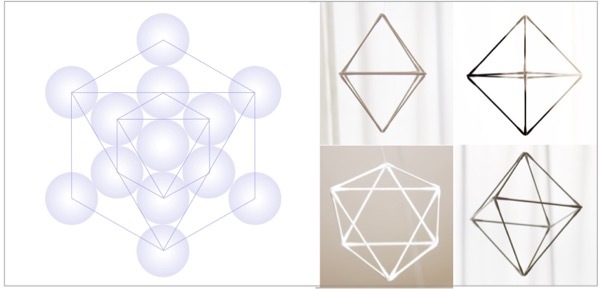
左のイラストは上のメタトロンキューブから何本かの線を整理して見やすくしたもの、右の4つの写真はそれを立体にしたものを様々な角度から見たもの。すべてまったく別のものに見えていますが、実はすべて同じものです。
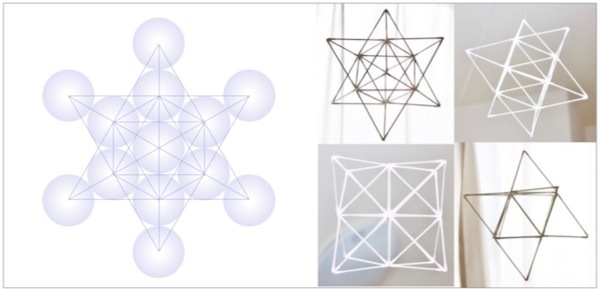
星型八面体、マカバと呼ばれているものです。
二次元に落とした形が左の図形、ダビデの星とか五芒星と呼ばれているものです。
立体である星型八面体は、正三角形を4つ組み合わせてできる四面体を上下逆さまに組み合わせるとあらわれます。
見えているすべての面が正三角形で、中央にある正八面体のすべての面を正四面体のトゲが覆っているような魅力的な立体幾何です。
美しいですね。
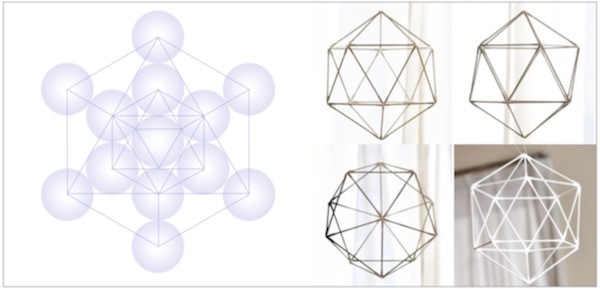
正二十面体。空間を正三角形20枚で囲むとできあがる形です。またまたこちらも角度を変えて眺めると次々に魅力的な姿があらわれます。
そして最後にこちら。
メタトロンキューブにあらわれた形は何を指しているのかちょっとわかりづらいのですが、立体にしてみるとなるほどの正八面体。
空間を正三角形8枚で囲むとできる形です。
この正八面体は上の星型八面体(ステラ・オクタンギュラ)のど真ん中にも入っています。
どうですか。
眺めれば眺めるほど魅力的で引き込まれますよね。
眺めていることも素晴らしいですが、これらをただ眺めるだけでなく「体験」するともっと様々なものがみえてきます。
上の図形はすべて、定規とコンパスと分度器があれば自分で描くことができます。

しかしこれらの幾何模様や立体幾何が内包する情報は、とてつもなく大きなものです。
そのための図工の会、ただ無心に作業する図工の会、子供のように遊ぶ会を、そのうちどこかでやりたいなあ、とうすらぼんやり考えています。
5月以降かなあ。
興味のある方はアンテナを張っておいてくださいませ。

